1. Basic Functioning

To perform a population synthesis of protoplanetary discs with Diskpop, the user needs to set up the simulation parameters in the user interface file, parameters.json. In this section we describe the general architecture of the code and mention some of the involved parameters, but refer to the following section for a detailed description of the parameters and their possible values.

A Diskpop simulation is composed of two key steps:

1. Generate a synthetic population of protoplanetary discs, with given initial conditions;

2. Evolve each disc in the population up to the given age via the chosen evolutionary prescription.

The user can entirely customize the initial conditions of the simulations, as well as decide whether to evolve the population solving the master equation numerically or analytically (where possible) and whether to set fixed parameters or perform a Monte Carlo extraction from a chosen distribution.

Note

The most realistic scenario would see a Monte Carlo extraction of the parameters that also take into account the observed correlations between them. However, both these options can be customized (find more details here)

1.1. Disc evolution

Diskpop is a 1D evolutionary code that considers all discs in a population independent and evolve them separately integrating the master evolution equation

(1)\[\frac{\partial \Sigma}{\partial t} = \frac{3}{r} \frac{\partial}{\partial r} \left[ \frac{1}{\Omega r} \frac{\partial}{\partial r} \left( r^2 \alpha_{\mathrm{SS}} \Sigma {c_s}^2 \right) \right] + \frac{3}{2r} \frac{\partial}{\partial r} \left[ \frac{\alpha_{\mathrm{DW}} \Sigma {c_s}^2}{\Omega} \right] - \frac{3 \alpha_{\mathrm{DW}} \Sigma {c_s}^2}{4 (\lambda-1)r^2 \Omega} - \dot{\Sigma}_{\mathrm{photo}},\]

which describes the time evolution of the gas surface density in the most general framework: \(\Sigma\) is the gas surface density, \(\Omega\) the Keplerian orbital frequency, \(\alpha_{\mathrm{SS}}\) the Shakura & Sunyaev (1973) \(\alpha\) parameter, \(\alpha_{\mathrm{DW}}\) the MHD equivalent of \(\alpha_{\mathrm{SS}}\) Tabone et al. (2022), \(c_s\) the sound speed, and \(\lambda\) the magnetic lever arm parameter, which quantifies the ratio of extracted to initial specific angular momentum. The four terms on the right hand side refer to

1. the viscous torque, whose strength is parameterised by \(\alpha_{\mathrm{SS}}\),

2. the wind-driven accretion, which corresponds to an advection term, parameterised by \(\alpha_{\mathrm{DW}}\),

3. mass loss due to MHD disc winds, parameterised by \(\lambda\) and

4. mass loss due to other physical phenomena (in our case, we consider internal and external photoevaporation).

Depending on the values of the specific parameters, Equation (1) can describe a purely viscous (\(\alpha_{\mathrm{DW}} = 0\)), purely MHD wind-driven (\(\alpha_{\mathrm{SS}} = 0\)) or hybrid (\(\alpha_{\mathrm{SS}}, \alpha_{\mathrm{DW}} \neq 0\)) evolution, with (\(\dot \Sigma_{\mathrm{photo}} \neq 0\)) or without (\(\dot \Sigma_{\mathrm{photo}} = 0\)) the influence of photoevaporation. In the following, we briefly describe the various evolutionary scenarios and the available analytical solutions, implemented in the code. Where an analytic solution is not available, Diskpop solves Equation (1) with the integration algorithm described in solution algorithm.

Purely viscous evolution

In the case of purely viscous evolution, the MHD winds parameter \(\alpha_{\mathrm{DW}}\) is set to zero. If we also neglect the influence of photoevaporation, Equation (1) reduces to the first term on the right hand side and its solution depends on the functional form of the effective viscosity, parameterised as \(\nu = \alpha_{\mathrm{SS}} c_s H\) (where \(H\) is the vertical height of the disc). A popular analytical solution for viscous discs is the Lynden-Bell & Pringle (1974) self-similar solution, which assumes viscosity to scale as a power-law of the radius (\(\nu \propto R^{\gamma}\)).

MHD winds-driven evolution

There are two classes of analytical solutions to Equation (1) in the MHD wind-driven scenario, associated with a specific prescription of \(\alpha_{\mathrm{DW}}\) (Tabone et al. 2022):

1. The simplest class of solutions (so-called hybrid solutions), which highlight the main features of wind-driven accretion in comparison to the viscous model, assume a constant \(\alpha_{\mathrm{DW}}`\) with time; these solutions depend on the value of \(\psi \equiv \alpha_{\mathrm{DW}}/\alpha_{\mathrm{SS}}\), which quantifies the relative strength of the radial and vertical torque.

2. Another class of solutions, which describe the unknown evolution of the magnetic field strength, assume a varying \(\alpha_{\mathrm{DW}}\) with time. To obtain these, Tabone et al. (2022) parameterised \(\alpha_{\mathrm{DW}}(t) \propto \Sigma_{\mathrm{c}} (t)^{-\omega}\), with \(\Sigma_{\mathrm{c}} = M_{\mathrm{d}}(t)/2 \pi {R_c}^2 (t)\) (where \(R_c\) is a characteristic radius) and \(\omega\) as a free parameter, and neglect the radial transport of angular momentum (\(\alpha_{\mathrm{SS}} = 0\)).

Photoevaporation

The generic \(\dot \Sigma_{\mathrm{photo}}\) term in Equation (1) allows to account for photoevaporative processes, both internal and external. The exact form of \(\dot \Sigma_{\mathrm{photo}}\) depends on the specific model considered; therefore, the availability (or lack thereof) of analytical solutions needs to be considered case by case.

1.2. Disc dispersal

Discs are considered dispersed when the gas surface density (or equivalently the mass) is too low to be detected. Depending on the evolutionary model considered, this is more or less likely to happen:

• in the viscous case, the disc mass naturally declines with time as a consequence of accretion onto the central star. However, this slow decline never results in complete disc dispersal - a classic problem of purely viscous evolution.

• in a viscous framework with internal photoevaporation, gas is removed from the disc as an effect of the ionization due to the radiation of the central protostar.

• in the MHD wind scenario, winds are launched from the disc surface and effectively remove mass from the total budget, resulting in the disc being dispersed after a few accretion timescales.

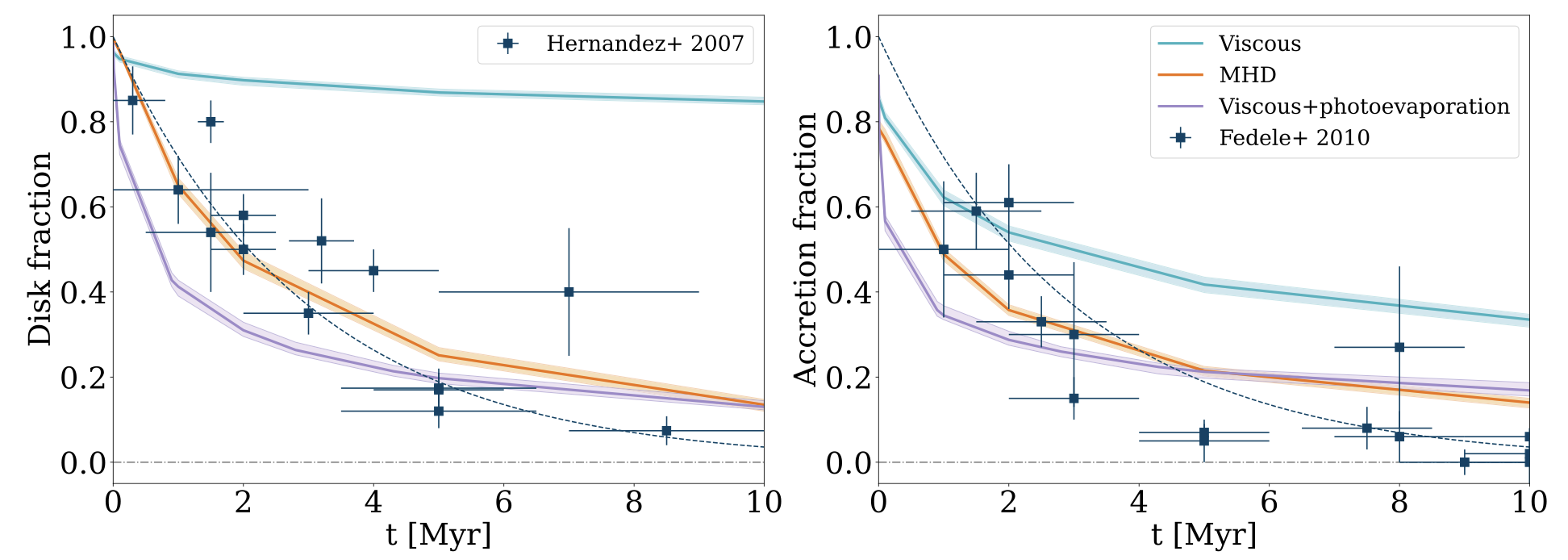
Decline of the disc-bearing (left) and accreting (right) objects over time in the viscous (blue), viscous+internal photoevaporation (orange) and wind-driven (lilac) model compared with the observational data.

The different impact of disc removal in the various evolutionary scenarios lead to a different evolution of the fraction of disc-bearing and accreting objects over time, as the figure above (from Somigliana et al. 2023) shows in the left and right panel respectively.